人工神经网络原理解析 | Lam的学习笔记

type

status

date

slug

summary

Part 1

何为人工神经网络

人工神经网络是模拟人脑的神经网络，用以实现人工智能的机器学习技术。我们知道，人脑可以说是世界上最复杂最精妙的系统之一，它由千亿计的神经元细胞组成。各个神经细胞相互链接，彼此之间传递电信号。从而造就了人类高于其他物种的思维能力。科学家受到人脑神经元的启发从而提出了人工神经网络的设想，使得人工智能的实现不再遥不可及。

生物神经元

关键部件：

树突 & 胞体 & 轴突

单个神经元的工作机制可以简单地描述为：树突接受其他神经元的神经末梢传来的电信号，信号传送到胞体并由某种机制决定是否激发下一次电信号的传递，若激发则电信号由轴突传递至神经末梢，再由神经末梢传递给其他神经元。其中，判断是否激发的机制有一大好处是可以减小神经元间微弱电信号（噪声）的干扰，使得自由足够强的电信号才能激发下一次传递。

人工神经元

概览

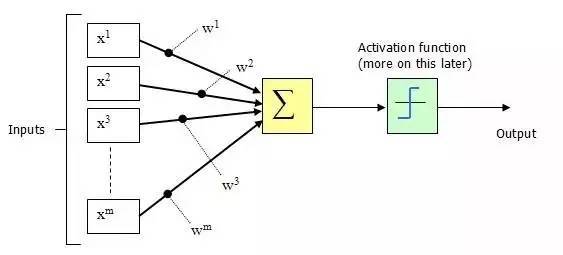
由生物神经元得到的启发，人工神经元与其大同小异。上图中：为该神经元树突所接受到的其他神经元传来的电信号。中间的圆圈为胞体，在胞体中将会由处理信号的机制，以决定输出信号y。

功能

在之前的生物神经元中已经说道，神经元对是否激发信号传递有一个判断机制，这是因为神经元不希望传递微小的噪声信号，而只传递有意识的明显信号。只有信号强度达到了某一个阙值，才会激发电信号的传递。那么在人工神经元中我们如何来实现这个机制呢？

这样的一个函数也许能够满足我们的需要：

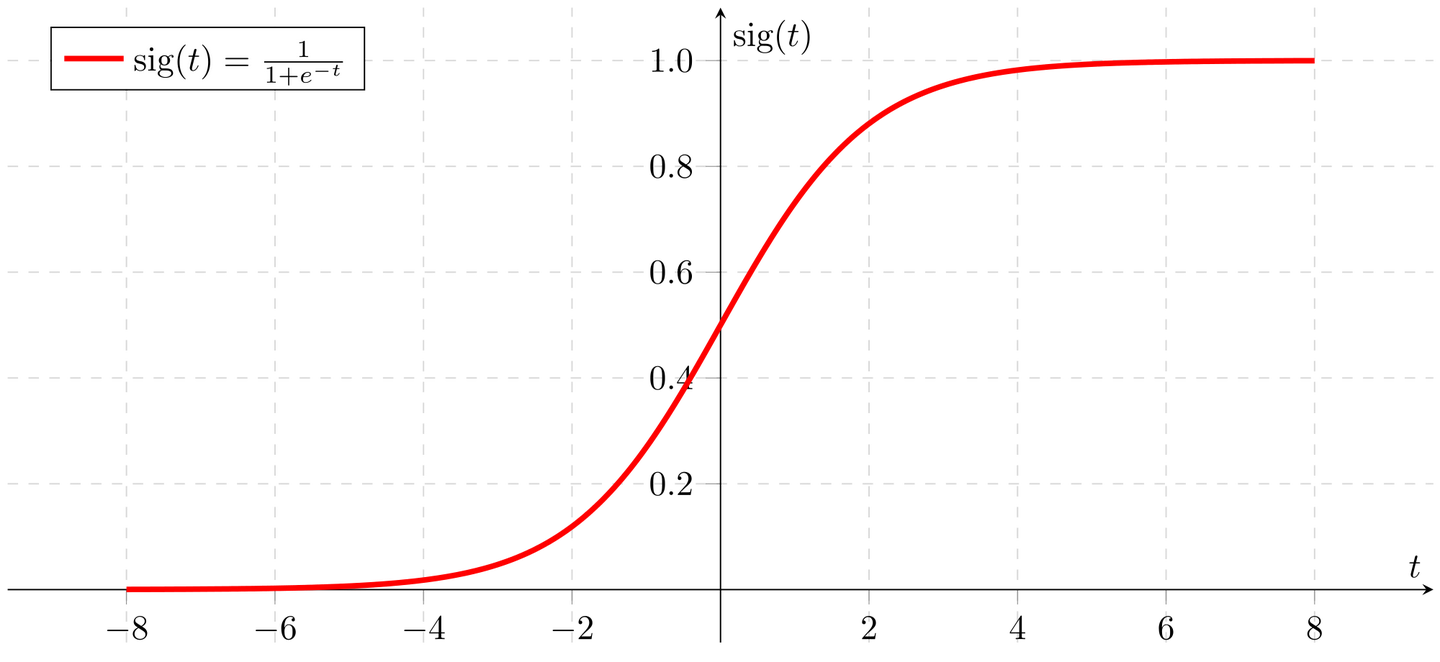
显而易见，这个简单的阶跃函数在输入信号大于T（阙值）时才会产生输出信号1（被激发），而较小的输入时输出为 0（被抑制）；我们称这样的函数为激活函数。当然，激活函数不会就只有这么一种。常用的还有sigmoid函数：

函数图像：
为输入信号
为权重值，表示各个输入信号对输出结果的影响力大小。对于为何引入权值可以做如下思考：你去相亲，你对未来对象的考量主要有身高，长相，身材，文化程度等，但遇到样样都好的概率实在是太底了，所以你决定适当放宽某些要求。比如如果学历高就可以降低身材长相的要求。这表示你比较注重伴侣的文化程度。因此，对方的文化程度对你的择偶有着重要的影响，其所占权重就会比较高。
求和函数将计算后将所得的值传给激活函数Sigmoid即：观察函数图不难发现，Sigmoid函数将加权求和的输入映射到0~1的值域内输出。

人工神经网络

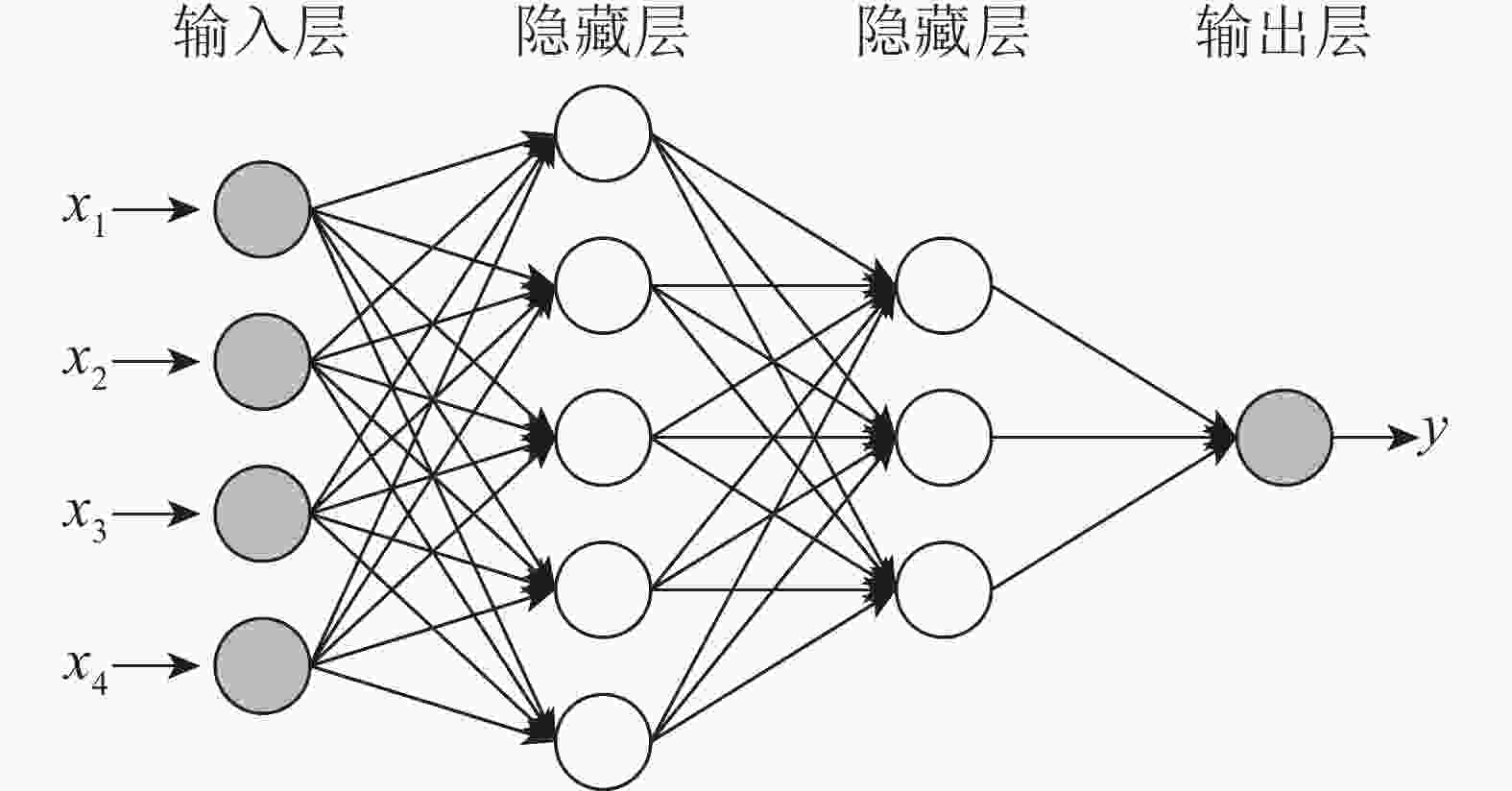
介绍完单个神经元的功能，如果把这些小部件组合起来，就成了所谓的人工神经网络。

层次结构：

输入层：接受外部输入信息，可以是图片等。

隐藏层：隐藏层层数不一，可根据需求来定。

输出层：将结果输出到外部。

链接方式：

除输入层外，每一层的每个神经元都接受其上一层所有神经元传来的信号的加权值。

神经元的链接方式并不唯一，你可以创造自己的链接方式，但为了便于抽象计算编码，规则的链接方式能帮我们大忙。

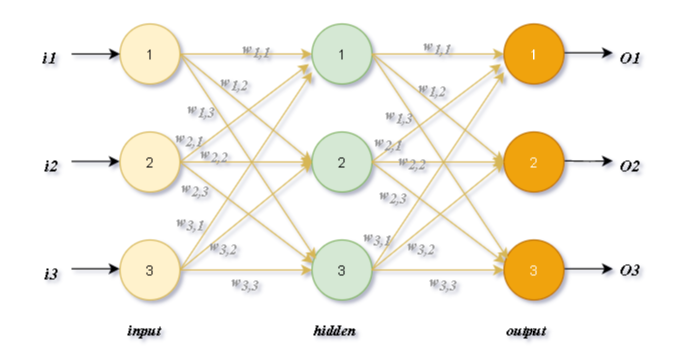
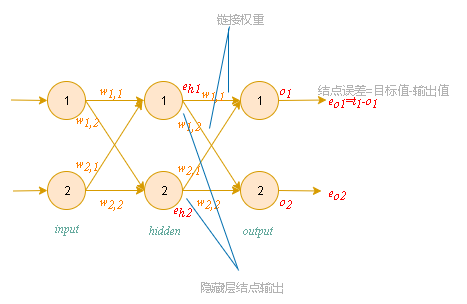
一个三层神经网络示例

参数释义：

为输入信号。

表示后层结点$j$与前一层节点$k$之间链接的权重值。

为该网络输出的结果信号。

信号的前向传播： 前面我们介绍了单个人工神经元对信号的处理。但是现在网络中有多个神经元，我们当然不愿意对每一个神经元节点都进行编码计算，因此我们将其简化为矩阵运算。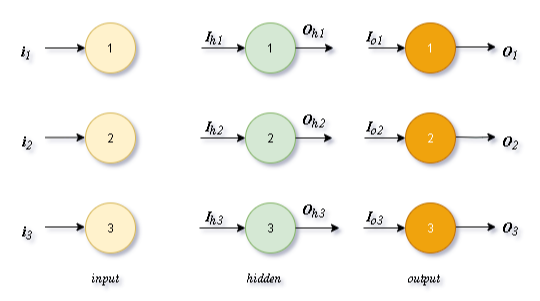

将输入看成一个多维列向量：

链接权重为一个的矩阵：

将两者相乘得到隐藏层的输入信号：

再将加权求和的信号值经过Sigmoid激活函数处理我们可以得到最终的输出向量：

这里需要注意的是，输入层到隐藏层的链接权重矩阵与隐藏层到输出成的链接权重矩阵是不同的矩阵。但是计算过程是一致的，因此同理可得：

到此，我们已经了解了神经网络中信号的前向传播机制，但是目前这个网络模型远远达不到我们的要求，它除了单纯的传播信号什么事情也做不了。显然后续我们得为其添加反馈机制，使其能够具有学习能力。

Part 2

如何让网络可以学习

上一篇文章中的神经网络还没有学习能力，这好比如说该网络只接收外部输入并输出结果，却没有反馈机制没有对结果进行正确性分析，让我们以小明与老师之间的对话来比喻这种情况：

老师：1+1=？

小明：6

老师：1+2=？

小明：2

可以发现，当小明给出答案后老师并没有给于他反馈。因此小明可能某一次猜中了正确答案，但只是凑巧而已，他不具备学习能力。现在让老师给点反馈：

老师：1+5=？

小明：4

老师：少了

小明：5

老师：少了

小明：6

老师：正确，你真棒！这样子，小明学会了1+5=6. 我们的神经网络也需要具备这样的学习能力。也就是说，当网络输出错误的结果时要有一个改变下一次输出的机制。想要改变输出，可以改变哪些量呢？观察输出函数：

不难发现，输出值与以下参数有关：

Sigmoid函数

链接权重

输入值

显然，我们不可能去左右网络的输入值，因为那是网络要求解的问题，不可能以改变问题的方式改变答案。那么改变激活函数sigmoid如何？这太麻烦了，试想那么多的神经元每一个都不同的激活函数会对运算造成大麻烦，将无法采用简洁的矩阵运算。因此，改变链接权重会是一个好办法。

学习能力的养成

我们已经知道可以通过改变链接权重来改变网络的输出值，使其符合预期。那么问题又来了：

改变权重的依据是什么？

如何改变？

改变的幅度多大合适？

改变的依据

改变权重的目的是让输出值与期望值越接近越好（误差值越小越好），因此误差就是依据。所谓误差就是期望值与网络输出值的差：

我们知道输出层的误差为：，但是其他层结点的误差是不知道的，因为其他层并没有一个输出期望值。不难发现，最终输出层造成的误差是所有层共同作用的结果，所以可以将总误差分摊给其他层。

误差的反向传播

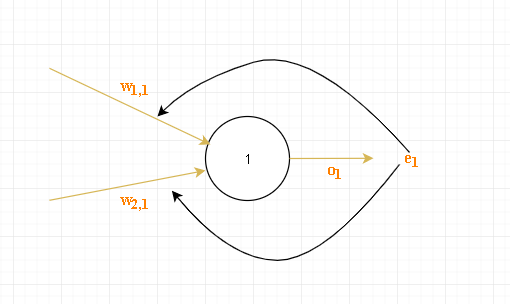
如上图误差为，因为链接权重越大说明对该误差的影响越大，因此以链接权重来决定每条链路所分摊误差的大小：

反向传播误差到更多层中：

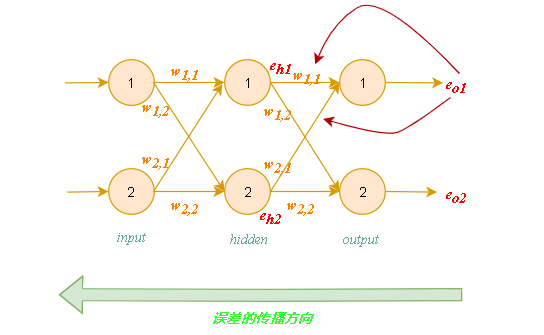
隐藏层结点的误差值：

使用矩阵乘法简化误差反向传播

误差向量：

隐藏层误差：

上述矩阵乘法太过复杂，无法通过简单的矩阵运算求解。观察上式可知，最重要的事情是输出误差链接权重$w_{j,k}$的乘法。较大的权重携带较大的误差给隐藏层，这些分数的分母是一种归一化因子。如果我们忽略掉这个因子，我们仅仅只是失去了后馈误差的真实值大小，但并没有失去其表示的真正含义（影响力）,也就是说反馈误差始终是以链接权重的强度来分配的。因此上式可以简化为：

不难发现，隐藏层至输出层的链接权重矩阵为:

因此：

到此我们得到了用矩阵来传播误差的算法：

到此，我们已经做了大量的工作了。我们计算出了所有层的误差，接下来的工作就是根据误差来调整链接权重了。

Part 3

如何更新权重

在上一篇文章中我们算出了各个层的误差，现在是时候利用这些误差来指导链接权重的修改了。那么该如何修改？

暴力枚举：对于一个三层的神经网络，每层有3个神经元结点，有两个的链接权重矩阵，共有18个权重值。假设每个权重在1和-1之间共有1000种取值，那么我们有种权重组合，这个数字已经很大了。但是，如果是每层有500个结点呢？那么权重数将达到个，将会有种组合。想要遍历这么些种可能得等到人类灭绝...

可见，暴力枚举并不能实际地解决我们的问题。

新的思路：让我们再次明确下我们的最终目的，让误差值降到最小。试着将其转化成数学上的求函数最小值问题。先前我们知道，误差是所有链接权重的函数:

现在我们需要额就是找出该函数的最小值。但由于真正的误差函数的自变量太多，先举个简单的例子：假设误差函数只有一个自变量（链接权重）：

其图像为：

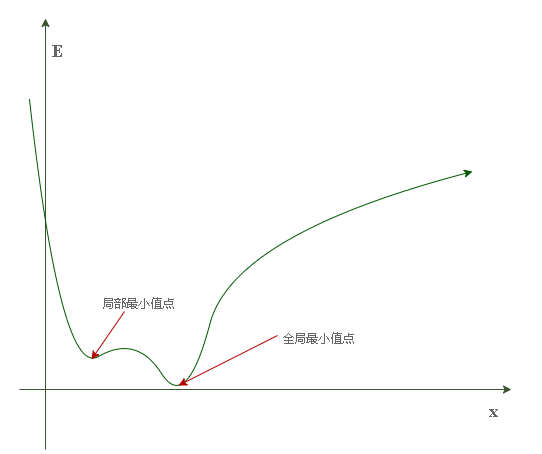
可以将其想象成一个连绵的山脉，有山峰也有山谷。设想将一个小球至于山腰，那么在重力的作用下它必定沿着所在位置的斜率方向向下滚动直到山谷。但是很明显，我们并没有重力帮忙，因此必须人为指定“滚动方向”。

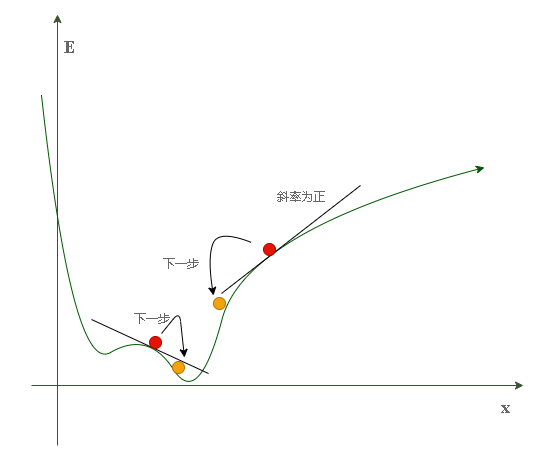
不难发现，当斜率为正时应向左滚动，斜率为负时应向右滚动。这种方法在数学上被称为梯度下降（gradient descent）。

可能的意外情况： 我们可能会碰到这种情况：当小球的起始位置为左侧山腰时，其很有可能最终会在局部最小值（右侧的第一个山谷）停下，这可不是我们所希望的结果。因为我们的目的是把误差降到最小，那里显然不是全局最小点（最深的山谷）。

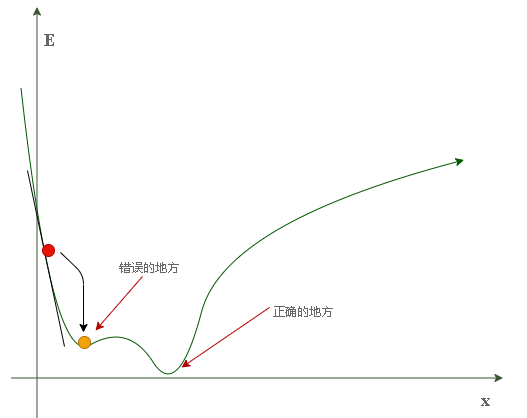
为了避免上述情况，我们应从不同的起始位置对神经网络进行多次训练，以确保其并不总是终止于错误的地方。而不同的起始位置意味着不同的链接权重。

选择误差函数的形式

可选项：

(目标值 - 期望值)

方差形式

我们选用方差形式，因为其具有很多优点：

可以很容易地使用代数方法（链式法则求解偏导数）计算出梯度下降的斜率

误差函数平滑连续，这使得梯度下降算法可以很好地发挥作用

越接近最小值梯度（斜率）越小，按照斜率调整步长可以减少越过最佳位置的风险

计算梯度值（斜率）

当只有一个链接权重时，误差函数为二维曲线：

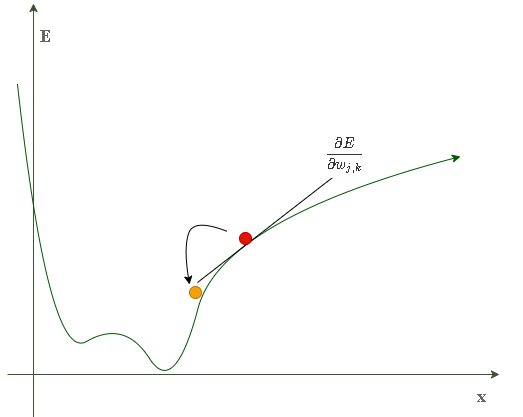
当有两个链接权重时，误差函数为一个三维曲面：

上述表达式表示了当权重改变时，误差是如何改变的。这是误差函数的斜率，也就是我们希望使用梯度下降的方法达到最小值的方向。

计算梯度：

在开始计算前我们回顾一下网络中各个参数的意义：

展开误差函数：由于一个结点的误差只与与其相连的链接权重有关，因此误差函数可以简单地表示为：

其中：所以:

所以：

其中：令

且：

因此，我们得到了以下表达式：

又由于我们只关心误差函数斜率的方向，因此可以将公式中的常数2省略，并不影响正负号：

改变链接权重

之前提到过，权重的改变方向与梯度的方向相反。因此我们规定权重的改变方式为：

参数释义：

为学习因子，可以调节这些权重变化的强度

用矩阵来简化运算：

将Sigmoid函数简化为输出：

到此，所有的前期工作都已完成。

Part 4

Python-numpy编码实现人工神经网络

前面的几篇文章我们熟悉了人工神经网络的数学原理及其推导过程，但有道是‘纸上得来终觉浅’，是时候将理论变为现实了。现在我们将应用Python语言以及其强大的扩充程序库Numpy来编写一个简单的神经网络。

准备数据：

训练集and测试集：Mnist手写数字数据集(复制git链接克隆)MINST数据库是由米国机器学习大佬Yann提供的手写数字数据库文件，其官方下载地址Download Mnist。该数据集将会是神经网络的输入信号。

每一张图片像素都为,因此可作为一个的向量传入神经网络。

初始花链接权重矩阵：使用正态概率分布采样权重，平均值为0，标准方差为结点传入链接数目的开方，即

编码实现

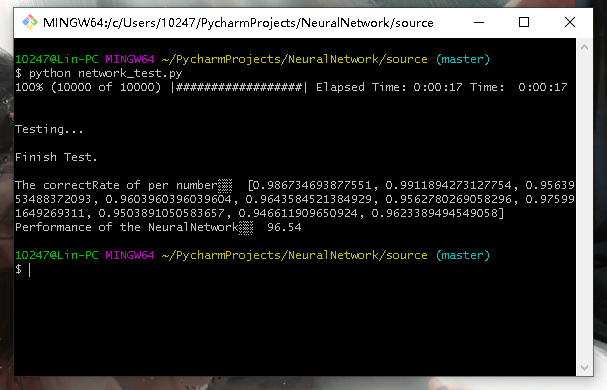
下面的代码实现了一个双隐层的神经网络，但是它的表现并不好（最起码在Mnist数据集的表现上差强人意），我训练了5个小时（5世代）也只能达到%96.54的准确率。相比而言当隐层的神经网络在Mnist数据集上的表现更好，三个小时（5世代）可以达到%97.34的准确率。你可以注释掉下面的部分代码将其退回到单隐层结构甚至加到三隐层结构。虽然代码写的很乱但代码中每一句都有详细的注释，别介意哈哈哈。包含两个源代码文件：

neural_network.py 包含神经网络主类用于训练神经网络

network_test.py 用于测试神经网络

neural_network.py

network_test.py

运行程序

cd进入代码所在文件夹

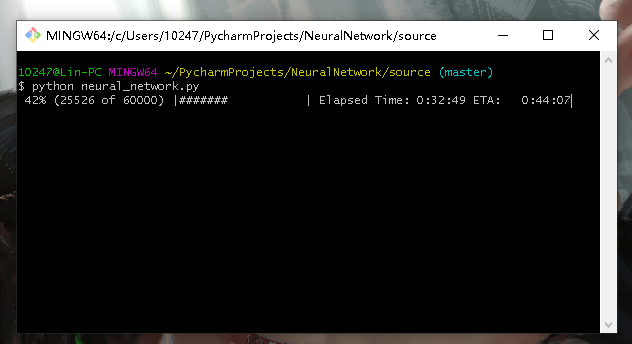
(训练神经网络)输入命令：neural_network.py

（测试神经网络）输入命令：network_test.py

💡

[Warning] 运行时请确保训练集和测试集数据的.csv文件与源代码文件在同一个目录下，否则请修改源码中的文件路径